In the paper Algorithmic QUBO Formulations for 𝑘-SAT and Hamiltonian Cycles a new approach is presented for how to formulate QUBOs.
Before reviewing the paper, let’s dicuss how QUBOs have been formulated previously. Let’s consider the the Graph Coloring problem for example: Let G(V,E) be a graph with vertices V and edges E and n different colors. The task in this problem is to decide if there is an assignment of vertices to colors such that no adjacent vertices in G have the same color. The QUBO formulation (Lucas 2014) is:
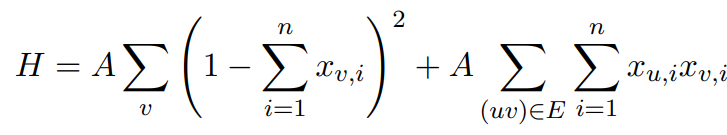
The formulation uses no control structures known from programming languages like loops, recursion or if-else statements. In our paper we, for the first time, show QUBO formulations for Max-k-SAT und Hamiltonian Cycles that do use these control structures and we demonstrate that by doing so we can create QUBO formulations that require much fewer qubits than previous formulations.
Satisfiability
Before we dive into the algorithmic QUBO formulation for k-SAT, let’s briefly introduce the k-SAT problem. SAT is short for Satisfiability and it is a well-known problem of computer science. Let V={a,b,c,…} be a set of boolean variables and let C be a set of clauses on V. A clause is a disjunction of literals and a literal is a boolean variable or its negation. Example for a clause containing 3 literals:
(a v -b v c)
SAT asks now if there is an assignment of truth values (True, False) to the boolean variables V such that every clause in C evaluates to True. k-SAT is a special case of SAT where every clause contains exactly k literals. k-SAT is known to be NP-complete for k > 2.
Algorithmic QUBO Formulation for k-SAT
Now let’s have a look at the general idea of our algorithmic QUBO formulation:
Let C be a clause consisting of k literals. This means there are 2k possible assignments, of which 2k – 1 assignments satisfy the clause and just one doesn’t. Example for the clause (a v -b v c):

The assignment (a=0, b=1, c=0) is the only one that doesn’t satisfy the clause.
The general idea is now: we need to find an boolean assignment for V. Therefore we will need QUBO variables xi for each variable V[i]. Now we need to formulate an energy landscape such that the assignment that satisfies all clauses has the minimum energy. We can do this by encoding each clause individually such that every assignment that satisfies the clause has energy e and the one assignment that does not satisfies the clause has energy e+1. Since this ensures that the global assignment that satisfies all clauses has energy E=|C| while all assignments that violate at least one clause have energy E>|C|.
To formulate a constraint that has energy e for all assignments that satisfy the clause and energy e+1 for the one assignment that doesn’t we need to use ancilla qubits for k>2. For k=3 we, for example, need 1 ancilla qubit (Chancellor et al. 2016). For k>3 we needed k ancilla qubits so far (Chancellor et al. 2016). In our paper we show that we just need log2(k+1) ancilla qubits.
We do this by „counting the number of literals that make a clause evaluate to True“. Since a clause is a disjunction of literals. Making a clause evalute to True requires at least one literal to evaluate to True (but it can also be 2 or more literals). Example for the clause (a v -b v c):
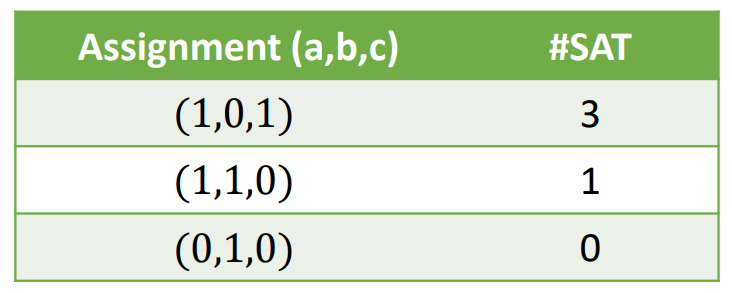
Using the assignment (a=1, b=0, c=1) all three literals of the clause (a v -b v c) evaluate to True, therefore #SAT=3. Using the assignment (a=1, b=1, c=0) only the literal a evaluates to True, therefore #SAT=1 and for (a=0, b=1, c=0) no literal of the clause evaluates to True.
Suppose we can encode the constraint for counting the number of literals that satisfy a clause using h=log2(k+1) ancillas (we can, see the paper), then we can continue recursively. Because ensuring that the clause is satisfied is equivalent to ensuring that #SAT>0. But #SAT is encoded into h binary variables. To ensure that #SAT>0 we therefore just need to ensure that at least one of the h binary variables is 1. This corresponds to another clause which only contains h literals. As an anchor of this recursion we can use the well-known formulations for 2-SAT or 3-SAT.
A detailed example is provided in the material of our tutorial we held at IEEE QCE Quantum Week 2023: Tutorial with detailed example
References
A direct mapping of Max k-SAT and high order parity checks to a chimera graph
Chancellor, Nicholas and Zohren, Stefan and Warburton, Paul A and Benjamin, Simon C and Roberts, Stephen
2016
Ising formulations of many NP problems
Andrew Lucas
2014